Algorithm flowcharted: Prime numbers

This article explains with flow charts the algorithm to create a list of prime numbers. The algorithm lists all prime numbers in a given range. Our algorithm is in Perl, but the principle is not language dependent.

Theory

A prime number is a natural number greater than 1 that cannot be formed by multiplying two smaller natural numbers. The first few prime numbers are 2, 3, 5, 7, 11, 13 and 17. As it happens, there is no upper limit.

Algorithm

It's easy to print a list of prime numbers. Simply go through all the numbers, check if they any of them is prime, and print it. We use a brute-force approach to determine if a number is prime.

Below is our prime script in Perl. As you run the script, it prints out all the prime numbers it finds. The printing usually happens on screen rather than on paper.

# Perl algorithm to print a list of prime numbers

# Maximum number to print
$max = 1000;

# Go through all integers 2..$max
for ($n = 2; $n <= $max; $n++) {
  # Assume $n is prime until proven wrong
  $isprime = 1;
  # Brute-force algorithm
  # See if $n is divisible by any smaller integer
  for ($i=2; $i<$n; $i++) {
    if ($n % $i == 0) {
      # $n is divisible by $i. Not prime.
      $isprime = 0;
      # Quit the loop
      last;
    }
  }
  # If $n is prime, print it
  print "$n " if $isprime;
  # Move on to next number
}

Flow chart

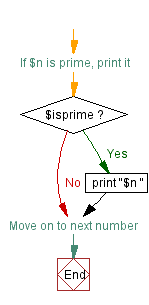
In flow chart form, the algorithm looks like this:

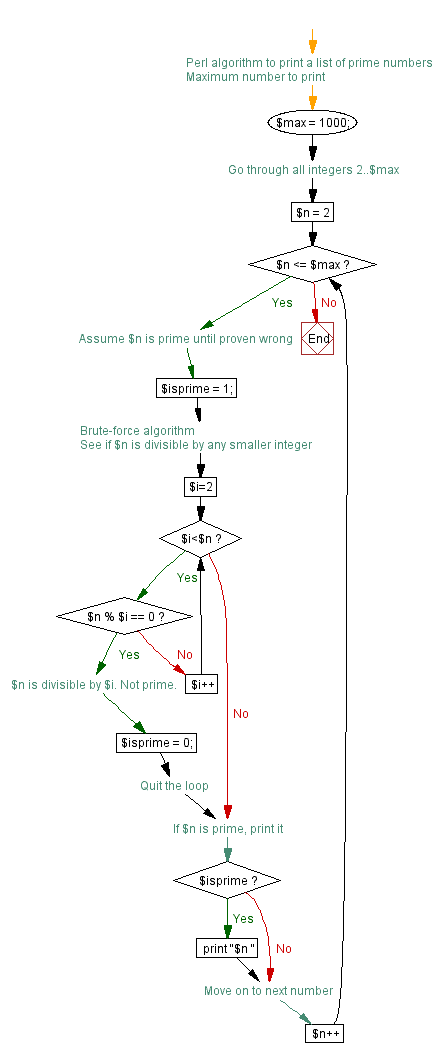
The flow charts on this page were created by Visustin, a flow chart tool that converts source code to flow charts.

Flow chart step by step

In this script, we look for prime numbers in the range 2..1000. For this reason, we set $max = 1000. Then we start looping through the numbers. We start from $n=2 and move towards 1000 one by one. On each round, we increment $n++ until we have reached $max. When that happens, we will have printed our list and the script ends.

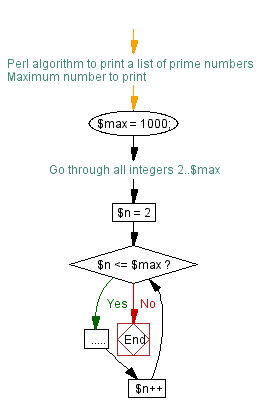
Inside the loop, for each number $n, we determine if it's prime or not. Here is how we do it.

Initially, we assume $n is prime, and therefore let $isprime=1. Then we attempt to prove $n is not prime. If it's not, we will let $isprime=0. In order to achieve this, starting from 2, we loop through all smaller numbers ($i) to see if $n is divisible by $i.

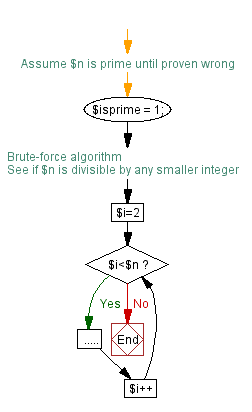
The chart below is an expanded version of the one above. Inside the loop, you can see how we determine if $n is divisible. The test $n % $i == 0 yields true if $n is divisible by $i. If the test is true, we execute the Yes branch, let $isprime=0 and immediately quit the loop by executing the last command.

On the other hand, if the test yields false, we execute the No branch, meaning we increment $i++ and move on to the next integer. We repeat this until the test yields true or no more integers are left. In the latter case, $isprime will have remained 1, and we have found a prime number.

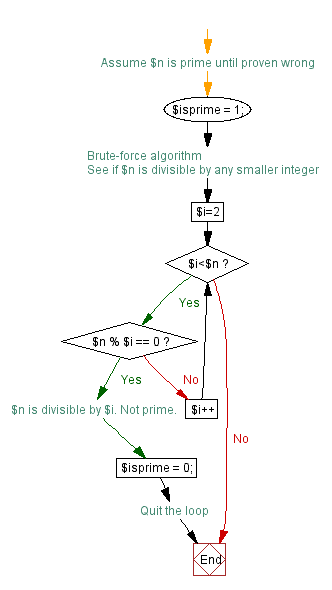
Last but not least, if we found a prime number, we print it out.

Output

2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199 211 223 227 229 233 239 241 251 257 263 269 271 277 281 283 293 307 311 313 317 331 337 347 349 353 359 367 373 379 383 389 397 401 409 419 421 431 433 439 443 449 457 461 463 467 479 487 491 499 503 509 521 523 541 547 557 563 569 571 577 587 593 599 601 607 613 617 619 631 641 643 647 653 659 661 673 677 683 691 701 709 719 727 733 739 743 751 757 761 769 773 787 797 809 811 821 823 827 829 839 853 857 859 863 877 881 883 887 907 911 919 929 937 941 947 953 967 971 977 983 991 997

The flow charts on this page were created by Visustin, a flow chart tool that converts source code to flow charts.